- LUMIÈRE - Diffraction
- LUMIÈRE - DiffractionOn dit qu’il y a diffraction quand, dans un milieu homogène et isotrope (même vitesse de propagation pour tous les rayons lumineux quelle que soit leur direction), la lumière ne se propage pas en ligne droite. Les phénomènes de diffraction ne se produisent que lorsque la lumière rencontre des trous ou des obstacles dont les dimensions sont de l’ordre de grandeur de la longueur d’onde; ils sont en contradiction avec les lois de l’optique géométrique. Il est en effet impossible de mettre en évidence la propagation rectiligne de la lumière: pour isoler un rayon, il faut diaphragmer un faisceau lumineux; or, la diffraction est d’autant plus importante que l’on cherche à mieux mettre en évidence la propagation rectiligne. Si l’on fait appel à la théorie quantique de la lumière, on aboutit à la même contradiction: plus on veut localiser un photon en disposant sur son trajet un diaphragme très petit, plus sa position, dans le plan d’observation, est mal définie (relation d’incertitude de Heisenberg).Depuis les travaux de Huygens, de Fresnel et de Fraunhofer, on classe les phénomènes de diffraction de la façon suivante:– Les phénomènes dits «à distance finie» (Fresnel); ce sont les phénomènes qui apparaissent dans l’ombre d’un obstacle quelconque (bord d’écran, fil...). La répartition des amplitudes diffractées s’obtient mathématiquement par une transformation de Fresnel.– Les phénomènes «à l’infini» (Fraunhofer), ainsi dénommés parce que leur calcul est particulièrement facile à exposer si l’on considère le cas particulier d’une onde plane limitée au contour d’un diaphragme et qu’on cherche l’amplitude diffractée dans une direction donnée, l’observation pouvant se faire pratiquement au foyer d’une lentille interposée sur le trajet de la lumière. Cette dénomination n’est pas excellente car les phénomènes de Fraunhofer peuvent s’observer à distance finie. La distinction est en fait la suivante: les phénomènes de Fresnel se produisent au voisinage de la limite de l’onde et sont éloignés de son centre de courbure; les phénomènes de Fraunhofer, au contraire, sont localisés au voisinage de l’image, c’est-à-dire au centre de courbure de l’onde. Ce sont ces derniers qu’on est amené à étudier pour déterminer la qualité des images optiques. Le traitement mathématique utilisé dans ce cas est une transformation de Fourier.1. Phénomènes de diffractionPrincipe de Huygens-FresnelLa diffraction fut découverte de façon fortuite en 1665 par un moine italien, Grimaldi, qui réalisa l’expérience suivante: une source ponctuelle éclaire un petit trou pratiqué dans un écran opaque, le contour de l’ombre projetée n’est pas net. On observe des franges de diffraction alternativement sombres et brillantes.Huygens fut le premier à interpréter la propagation de la lumière en imaginant un mécanisme manifestement inspiré par l’étude de la propagation d’ébranlements mécaniques (tels que les rides à la surface de l’eau) et en considérant une action de proche en proche entre les divers points de l’espace. La fécondité de ce point de vue n’est clairement apparue que lorsque Fresnel (1815) montra que les phénomènes de diffraction ne sont autres que des phénomènes interférentiels qui s’expliquent grâce à la théorie ondulatoire de la lumière.Huygens avait formulé l’hypothèse que les ébranlements répartis sur une surface d’onde à l’instant t jouent le rôle de sources secondaires émettant à leur tour des ébranlements qui se propagent à partir de divers points de l’onde; l’ensemble de ces ondelettes doit évidemment donner naissance à la surface d’onde à un instant ultérieur t (fig. 1); celle-ci apparaît finalement comme l’enveloppe des diverses ondelettes. Fresnel (1815) précisa ce principe en supposant que l’on peut calculer l’amplitude des ébranlements en tout point de l’espace en combinant les vibrations diffractées par les divers éléments de la surface d’onde: l’amplitude diffractée en un point M de l’espace par un élément de surface d’onde voisin de S doit être proportionnelle à l’amplitude reçue en S (généralement constante) et inversement proportionnelle à la distance SM, comme pour une source primaire située en S. D’autre part, la phase de la vibration en M s’exprime simplement à l’aide du chemin optique SM. Ainsi la vibration reçue en un point M est la somme d’une infinité de vibrations émises par des sources fictives réparties sur la surface d’onde initiale. Cette façon de voir s’est révélée extrêmement féconde; elle a permis d’interpréter les phénomènes de diffraction.Le principe de Huygens-Fresnel, sous cette forme élémentaire, est cependant critiquable; en particulier, les sources réparties sur la surface d’onde devraient donner naissance non seulement à une onde progressive dans la direction de propagation, mais aussi à une onde réfléchie, renvoyée vers l’arrière. Kirchhoff (1824-1887) a le premier donné une justification mathématique de ce principe, en même temps qu’il fournissait une expression correcte de l’amplitude diffractée par chaque élément de surface d’onde, qui éliminait la possibilité d’une onde réfléchie. Cependant, l’expression donnée par Kirchhoff convient aux ondes scalaires (ondes sonores par exemple) mais non aux ondes électromagnétiques, qui sont transversales. D’assez nombreuses expressions du principe de Huygens utilisables dans ce cas ont été proposées; elles donnent une justification du vieux principe, satisfaisante dans le cas des ondes électromagnétiques, complète pour l’immense majorité des problèmes de diffraction où l’on peut faire les approximations suivantes:– l’amplitude du rayonnement émis par les sources secondaires est indépendante de la direction, c’est-à-dire de l’angle de diffraction (à condition que cet angle reste petit);– les écrans n’apportent à l’onde aucune perturbation (sinon la suppression des parties masquées); on ne tient pas compte de leurs propriétés spécifiques telles que la conductibilité électrique.Expression mathématique du principe de HuygensConsidérons une source ponctuelle S de lumière monochromatique () qui éclaire une ouverture de dimensions finies, pratiquées dans un écran opaque ( 神) (fig. 2). Soit P(x , y ) un point courant à l’intérieur du contour C de l’ouverture. L’amplitude au point P, considéré comme une source secondaire, est de la forme:
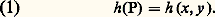 h (x , y ) est une fonction réelle ou complexe identiquement nulle en dehors du contour C de la pupille. La vibration envoyée par P, lorsqu’elle arrive au point M( 﨡, 兀), a pour amplitude:
h (x , y ) est une fonction réelle ou complexe identiquement nulle en dehors du contour C de la pupille. La vibration envoyée par P, lorsqu’elle arrive au point M( 﨡, 兀), a pour amplitude: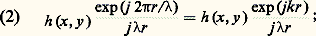 en posant:
en posant: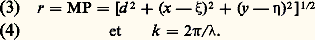 Le champ émis par un petit élément d S de la pupille est proportionnel à d S et le champ total au point M sera donné par:
Le champ émis par un petit élément d S de la pupille est proportionnel à d S et le champ total au point M sera donné par: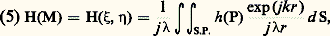 où S.P. désigne la surface de la pupille.Cette formule sert de point de départ pour tous les calculs de diffraction.Classification des phénomènes de diffractionQuelle que soit la position du plan d’observation ( 神 ), on n’observe jamais une image lumineuse ponctuelle, identique à la source, mais une tache de diffraction d’autant plus étalée que la diaphragmation de l’onde incidente par la pupille ( 神) est plus importante. La formule (5) est absolument générale et permet de traiter tous les phénomènes de diffraction. Toutefois, les expériences peuvent se diviser en deux classes, sans que la distinction soit absolument rigide.Diffraction de FresnelLa diffraction de Fresnel apparaît lorsque le plan ( 神 ) est placé à distance finie de la pupille diffractante (fig. 3). Il n’est pas besoin d’utiliser de système optique dans le montage, c’est uniquement le mécanisme de la formation des ombres qui est en cause. (De telles ombres peuvent aussi s’observer avec un instrument d’optique lorsque le plan d’observation 神 est éloigné du plan image). L’expérience la plus simple consiste à placer un écran à bord rectiligne dans un faisceau lumineux émis par une source ponctuelle; on constate que l’éclairement dans le plan d’observation croît progressivement, même lorsqu’on est encore dans l’ombre géométrique: lorsqu’on atteint la limite de l’ombre, il n’est encore égal qu’au quart de l’éclairement normal; il continue ensuite à croître, mais n’atteint la valeur asymptotique qu’à grande distance du bord de l’ombre; il passe au préalable par une série de maxima et de minima qui constituent les franges classiques de Fresnel (fig. 4). Des franges analogues peuvent être observées dans l’ombre d’une fente, d’un fil... (fig. 5).Pendant longtemps ces phénomènes n’ont connu qu’un intérêt historique: c’était par eux que Fresnel avait vérifié ses idées sur l’origine des phénomènes de diffraction; avec l’holographie , ils ont acquis une importance particulière. L’holographie est un procédé photographique permettant d’obtenir une image en relief d’un objet à trois dimensions; il suffit pour cela d’enregistrer une onde électromagnétique sur une plaque photographique située dans un plan quelconque, sans intervention d’un système optique.Les phénomènes de diffraction ne sont observables que lorsque les dimensions de la pupille sont petites par rapport à la distance d. La tache de diffraction ayant aussi des dimensions inférieures à d , on peut transformer l’expression de r et écrire:
où S.P. désigne la surface de la pupille.Cette formule sert de point de départ pour tous les calculs de diffraction.Classification des phénomènes de diffractionQuelle que soit la position du plan d’observation ( 神 ), on n’observe jamais une image lumineuse ponctuelle, identique à la source, mais une tache de diffraction d’autant plus étalée que la diaphragmation de l’onde incidente par la pupille ( 神) est plus importante. La formule (5) est absolument générale et permet de traiter tous les phénomènes de diffraction. Toutefois, les expériences peuvent se diviser en deux classes, sans que la distinction soit absolument rigide.Diffraction de FresnelLa diffraction de Fresnel apparaît lorsque le plan ( 神 ) est placé à distance finie de la pupille diffractante (fig. 3). Il n’est pas besoin d’utiliser de système optique dans le montage, c’est uniquement le mécanisme de la formation des ombres qui est en cause. (De telles ombres peuvent aussi s’observer avec un instrument d’optique lorsque le plan d’observation 神 est éloigné du plan image). L’expérience la plus simple consiste à placer un écran à bord rectiligne dans un faisceau lumineux émis par une source ponctuelle; on constate que l’éclairement dans le plan d’observation croît progressivement, même lorsqu’on est encore dans l’ombre géométrique: lorsqu’on atteint la limite de l’ombre, il n’est encore égal qu’au quart de l’éclairement normal; il continue ensuite à croître, mais n’atteint la valeur asymptotique qu’à grande distance du bord de l’ombre; il passe au préalable par une série de maxima et de minima qui constituent les franges classiques de Fresnel (fig. 4). Des franges analogues peuvent être observées dans l’ombre d’une fente, d’un fil... (fig. 5).Pendant longtemps ces phénomènes n’ont connu qu’un intérêt historique: c’était par eux que Fresnel avait vérifié ses idées sur l’origine des phénomènes de diffraction; avec l’holographie , ils ont acquis une importance particulière. L’holographie est un procédé photographique permettant d’obtenir une image en relief d’un objet à trois dimensions; il suffit pour cela d’enregistrer une onde électromagnétique sur une plaque photographique située dans un plan quelconque, sans intervention d’un système optique.Les phénomènes de diffraction ne sont observables que lorsque les dimensions de la pupille sont petites par rapport à la distance d. La tache de diffraction ayant aussi des dimensions inférieures à d , on peut transformer l’expression de r et écrire: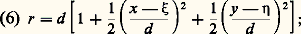 l’équation (5) où, au dénominateur, on peut remplacer r par d devient (après suppression du terme constant exp.(jkd ), grâce à un changement d’origine des phases):
l’équation (5) où, au dénominateur, on peut remplacer r par d devient (après suppression du terme constant exp.(jkd ), grâce à un changement d’origine des phases):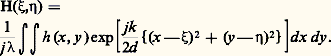 Par la suite, le terme constant l/(j) sera sous-entendu et on écrira:
Par la suite, le terme constant l/(j) sera sous-entendu et on écrira: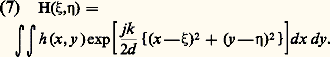 Cette intégrale est une opération mathématique, appelée transformation de Fresnel.Diffraction de FraunhoferLa diffraction de Fraunhofer intervient dans toutes les images optiques. Un instrument d’optique, même d’excellente qualité (dépourvu d’aberration), ne donne jamais une image conforme à l’objet: toute image optique est entachée de diffraction. Considérons l’objet le plus simple: un point lumineux S. Il émet une onde sphérique 0, divergente, de rayon d 0, centrée en S. L’objectif transforme cette onde divergente en une onde sphérique convergente , de rayon d , centrée sur l’image géométrique S (fig. 6). Si l’on tenait compte uniquement des lois de l’optique géométrique (onde non limitée), l’image S serait parfaitement ponctuelle. En réalité l’onde est limitée par le contour de la pupille de sortie de l’instrument. Avant traversée de la pupille, la répartition des amplitudes dans le plan ( 神) est donnée par:
Cette intégrale est une opération mathématique, appelée transformation de Fresnel.Diffraction de FraunhoferLa diffraction de Fraunhofer intervient dans toutes les images optiques. Un instrument d’optique, même d’excellente qualité (dépourvu d’aberration), ne donne jamais une image conforme à l’objet: toute image optique est entachée de diffraction. Considérons l’objet le plus simple: un point lumineux S. Il émet une onde sphérique 0, divergente, de rayon d 0, centrée en S. L’objectif transforme cette onde divergente en une onde sphérique convergente , de rayon d , centrée sur l’image géométrique S (fig. 6). Si l’on tenait compte uniquement des lois de l’optique géométrique (onde non limitée), l’image S serait parfaitement ponctuelle. En réalité l’onde est limitée par le contour de la pupille de sortie de l’instrument. Avant traversée de la pupille, la répartition des amplitudes dans le plan ( 神) est donnée par: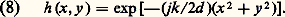 La diffraction n’intervient qu’après traversée de la pupille. La répartition des amplitudes dans le plan image ( 神 ) peut s’écrire, à partir de (7):
La diffraction n’intervient qu’après traversée de la pupille. La répartition des amplitudes dans le plan image ( 神 ) peut s’écrire, à partir de (7):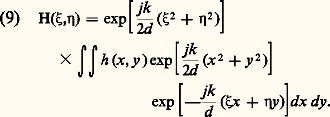 Compte tenu de (8) cette équation devient:
Compte tenu de (8) cette équation devient: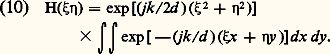 Si l’on place dans le plan ( 神) un filtre (réseau, cliché photographique...) dont la transparence n’est pas uniforme, mais caractérisée par la fonction f (x , y ), on a, de façon générale:
Si l’on place dans le plan ( 神) un filtre (réseau, cliché photographique...) dont la transparence n’est pas uniforme, mais caractérisée par la fonction f (x , y ), on a, de façon générale: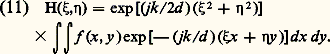 En résumé, si la répartition des amplitudes dans le plan pupillaire ( 神) est:
En résumé, si la répartition des amplitudes dans le plan pupillaire ( 神) est: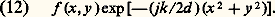 La répartition des amplitudes dans le plan image ( 神 ) s’écrit:
La répartition des amplitudes dans le plan image ( 神 ) s’écrit: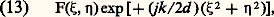 en posant:
en posant: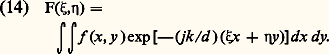 Si on effectue le changement de variables:
Si on effectue le changement de variables: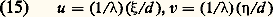 on obtient:
on obtient: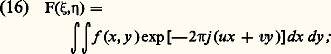 u et v sont les coordonnées réduites de l’espace de Fourier. On dit que F (u , v) est le spectre de f (x , y ).Les calculs se simplifient et les facteurs de phase quadratiques de (12) et (13) disparaissent si l’on peut considérer des ondes planes , c’est-à-dire si la distance d est grande ou si les dimensions de la pupille ou de la zone d’observation permettent d’assimiler les ondes sphériques à leur plan tangent sur l’axe.La formule (16) est encore valable à condition de poser:
u et v sont les coordonnées réduites de l’espace de Fourier. On dit que F (u , v) est le spectre de f (x , y ).Les calculs se simplifient et les facteurs de phase quadratiques de (12) et (13) disparaissent si l’on peut considérer des ondes planes , c’est-à-dire si la distance d est grande ou si les dimensions de la pupille ou de la zone d’observation permettent d’assimiler les ondes sphériques à leur plan tangent sur l’axe.La formule (16) est encore valable à condition de poser: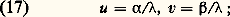 見 et 廓 étant les cosinus directeurs des rayons diffractés.Dans ces conditions, la diffraction de Fraunhofer porte le nom de diffraction à l’infini .Diffraction par des pupilles de forme simpleF(u , v) se déduit de f (x , y ) par une transformation de Fourier. Cette transformation est réciproque; inversement, connaissant F(u , v), on peut en déduire f (x , y ) par la transformation inverse:
見 et 廓 étant les cosinus directeurs des rayons diffractés.Dans ces conditions, la diffraction de Fraunhofer porte le nom de diffraction à l’infini .Diffraction par des pupilles de forme simpleF(u , v) se déduit de f (x , y ) par une transformation de Fourier. Cette transformation est réciproque; inversement, connaissant F(u , v), on peut en déduire f (x , y ) par la transformation inverse: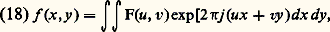 ce qui peut encore s’écrire d’une façon plus formelle:
ce qui peut encore s’écrire d’une façon plus formelle: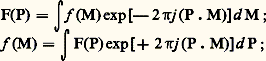 ou bien encore:
ou bien encore: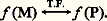 P et M désignent les vecteurs OPet 諸 ぬ et P. M leur produit scalaire.On va étudier les figures de diffraction de quelques pupilles de formes simples et de transparence uniforme.
P et M désignent les vecteurs OPet 諸 ぬ et P. M leur produit scalaire.On va étudier les figures de diffraction de quelques pupilles de formes simples et de transparence uniforme.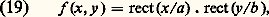
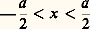 et à 0 partout ailleurs. On en déduit:
et à 0 partout ailleurs. On en déduit: On observe dans le plan ( 神 ) une sorte de quadrillage (fig. 7 a).Supposons qu’une des dimensions soit beaucoup plus grande que l’autre, par exemple a 礪礪 b , la pupille est une fente de surface s ; la formule (20) devient alors:
On observe dans le plan ( 神 ) une sorte de quadrillage (fig. 7 a).Supposons qu’une des dimensions soit beaucoup plus grande que l’autre, par exemple a 礪礪 b , la pupille est une fente de surface s ; la formule (20) devient alors: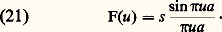 Il faut noter que l’amplitude est proportionnelle à la surface de la pupille, alors que l’éclairement est proportionnel au carré de la surface de la pupille.Si on désigne par i l’angle que fait le rayon diffracté avec la normale à la fente, on a:
Il faut noter que l’amplitude est proportionnelle à la surface de la pupille, alors que l’éclairement est proportionnel au carré de la surface de la pupille.Si on désigne par i l’angle que fait le rayon diffracté avec la normale à la fente, on a: L’amplitude diffractée dans la direction i est de la forme:
L’amplitude diffractée dans la direction i est de la forme: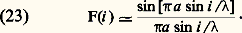 F(i ) écrit sous cette forme est dit normalisé.Seule la droite O 﨡 perpendiculaire à la plus grande dimension de la fente est éclairée. La répartition des éclairements suivant cette droite est donnée par la figure 7 b. Le maximum central a pour largeur:
F(i ) écrit sous cette forme est dit normalisé.Seule la droite O 﨡 perpendiculaire à la plus grande dimension de la fente est éclairée. La répartition des éclairements suivant cette droite est donnée par la figure 7 b. Le maximum central a pour largeur: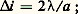 il est placé sur l’image géométrique S et est deux fois plus large que les maxima latéraux.Le cas de l’ouverture circulaire est très courant en optique, où la diaphragmation provient de la monture des lentilles. Soit D le diamètre de l’ouverture. La tache de diffraction est appelée tache d’Airy, du nom de l’astronome anglais (1801-1892) qui la découvrit. Elle présente la même symétrie de révolution que la pupille. On observe un maximum de lumière centré sur S et entouré d’anneaux alternativement noirs et brillants (fig. 7 c). Si on pose:
il est placé sur l’image géométrique S et est deux fois plus large que les maxima latéraux.Le cas de l’ouverture circulaire est très courant en optique, où la diaphragmation provient de la monture des lentilles. Soit D le diamètre de l’ouverture. La tache de diffraction est appelée tache d’Airy, du nom de l’astronome anglais (1801-1892) qui la découvrit. Elle présente la même symétrie de révolution que la pupille. On observe un maximum de lumière centré sur S et entouré d’anneaux alternativement noirs et brillants (fig. 7 c). Si on pose: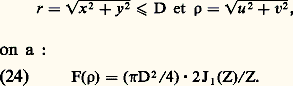 J1 désigne la fonction de Bessel d’ordre 1 et Z = 神福D. Le pic central a pour rayon angulaire: 1,22/D.Propriétés générales reliant la pupille et la figure de diffractionSupposons que, sur une pupille de transmission f (x , y ) on effectue des affinités de rapport m suivant ox et n suivant oy. La fonction de transmission de la nouvelle pupille est:
J1 désigne la fonction de Bessel d’ordre 1 et Z = 神福D. Le pic central a pour rayon angulaire: 1,22/D.Propriétés générales reliant la pupille et la figure de diffractionSupposons que, sur une pupille de transmission f (x , y ) on effectue des affinités de rapport m suivant ox et n suivant oy. La fonction de transmission de la nouvelle pupille est: L’amplitude de la nouvelle figure de diffraction s’écrit:
L’amplitude de la nouvelle figure de diffraction s’écrit: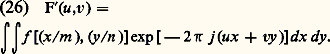
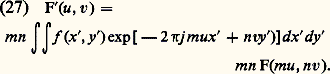 La nouvelle figure de diffraction se déduit de l’ancienne en multipliant u et v respectivement par m et n. En résumé, toute dilatation de la pupille suivant une direction quelconque se traduit par une contraction de la figure de diffraction suivant la même direction. On voit l’intérêt d’utiliser des objectifs aussi «ouverts» que possible.Il est évident que si la pupille tourne dans son plan il en est de même de la figure de diffraction.Supposons qu’on applique à la pupille une translation x 0, y 0, c’est-à-dire qu’on change x en x = x + x 0 et y en y = y + y 0. On a alors:
La nouvelle figure de diffraction se déduit de l’ancienne en multipliant u et v respectivement par m et n. En résumé, toute dilatation de la pupille suivant une direction quelconque se traduit par une contraction de la figure de diffraction suivant la même direction. On voit l’intérêt d’utiliser des objectifs aussi «ouverts» que possible.Il est évident que si la pupille tourne dans son plan il en est de même de la figure de diffraction.Supposons qu’on applique à la pupille une translation x 0, y 0, c’est-à-dire qu’on change x en x = x + x 0 et y en y = y + y 0. On a alors: c’est-à-dire:
c’est-à-dire: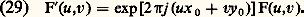 L’amplitude F(u , v) est multipliée par le facteur de phase linéaire: exp [2 神j (ux 0 + vy 0)]. Par contre l’éclairement, dans la tache de diffraction, reste inchangée:
L’amplitude F(u , v) est multipliée par le facteur de phase linéaire: exp [2 神j (ux 0 + vy 0)]. Par contre l’éclairement, dans la tache de diffraction, reste inchangée: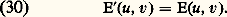 La figure de diffraction reste immobile dans le plan ( 神 ), centrée sur l’image géométrique, quand on translate la pupille dans le plan ( 神).Jusqu’à présent, on a supposé que la source S était située sur l’axe de l’instrument. Si S n’est plus au foyer principal de L0, les rayons incidents ont pour cosinus directeurs 見0 et 廓0. La différence de marche entre les deux rayons diffractés dans la même direction (x , 廓), l’un passant par O, l’autre par P, est:
La figure de diffraction reste immobile dans le plan ( 神 ), centrée sur l’image géométrique, quand on translate la pupille dans le plan ( 神).Jusqu’à présent, on a supposé que la source S était située sur l’axe de l’instrument. Si S n’est plus au foyer principal de L0, les rayons incidents ont pour cosinus directeurs 見0 et 廓0. La différence de marche entre les deux rayons diffractés dans la même direction (x , 廓), l’un passant par O, l’autre par P, est: La répartition des amplitudes dans l’image est alors:
La répartition des amplitudes dans l’image est alors: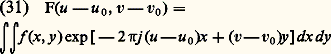 La figure de diffraction a pour centre: u = u 0, v=v0. Elle suit l’image géométrique de la source dans ses déplacements.Diffraction inverseÀ partir des caractéristiques de l’objet et des pupilles, on peut déterminer la répartition des amplitudes dans l’image. Le problème de la diffraction inverse consiste à déduire les caractéristiques de l’objet à partir des ondes diffractées et enregistrées par le détecteur.2. Les réseauxDescriptionD’une façon générale, un réseau est une surface, transparente ou réfléchissante, présentant une perturbation périodique. Les réseaux possèdent la propriété de disperser la lumière. (Tout le monde a pu observer les spectres colorés qui entourent les ampoules de lampadaires, la nuit, lorsqu’on regarde ceux-ci à travers la trame régulière d’un voilage de fenêtre.)Les premiers réseaux, inventés par Fraunhofer, étaient constitués par des fils équidistants tendus entre deux supports; Fraunhofer bobinait un fil fin entre deux tiges filetées parallèles, soudait les fils sur les tiges, et coupait une des deux nappes de fils ainsi constituées. On peut considérer de tels réseaux comme une série de fentes parallèles et équidistantes; on les utilisait par transmission.Ensuite les réseaux furent fabriqués en gravant, sur une surface de verre ou de métal réfléchissant, une série de sillons équidistants, au moyen d’un diamant; on obtient ainsi des réseaux par transmission, ou par réflexion, difficilement assimilables à une série de fentes, mais dont on peut dire qu’ils ont une structure périodique.Actuellement on fabrique surtout des réseaux par réflexion, obtenus en gravant une série de sillons équidistants dans une mince couche d’aluminium déposée sur une plaque de verre; cette couche d’aluminium étant relativement tendre, on peut, sans que l’usure modifie le profil du diamant traceur, tracer un grand nombre de sillons de profil exactement déterminé à l’avance. On peut d’ailleurs facilement faire des répliques des réseaux ainsi fabriqués par gravure et dont le prix de revient serait trop élevé. La réplique d’un réseau original s’obtient en versant sur le réseau une solution de collodion dans l’éther. Après évaporation de l’éther, on détache du réseau une pellicule transparente qui en reproduit les traits. Une réplique transparente peut être transformée en réplique utilisable par réflexion en y déposant une mince couche métallique par évaporation sous vide.Récemment une technique toute différente, utilisant la photographie, a été mise au point. On obtient un réseau sinusoïdal en enregistrant sur une émulsion photosensible un interférogramme; il suffit de photographier le champ d’un interféromètre à deux ondes, éclairé par une source très monochromatique (un laser). Toutefois, il faut utiliser des plaques spéciales, dites plaques holographiques , qui possèdent une très haute résolution (1 200 à 1 500 traits par mm).Si l’on éclaire un réseau par un faisceau provenant d’une source ponctuelle infiniment éloignée (ou placée au foyer d’une lentille collimatrice), on trouve qu’il y a de la lumière réfléchie (ou transmise) non seulement dans la direction de réflexion régulière (ou de transmission rectiligne), mais aussi dans un certain nombre d’autres directions très bien déterminées qui sont des maxima d’interférences. Or les positions de ces maxima dépendent de la longueur d’onde: on obtient ainsi une dispersion. On ne considérera que des réseaux présentant une perturbation périodique suivant une dimension; on peut alors remplacer la source ponctuelle par une fente parallèle aux sillons du réseau: cette fente est placée dans le plan focal d’une lentille L1, et l’observation s’effectue dans le plan focal d’une lentille L2 placée après le réseau. Si on éclaire la fente en lumière polychromatique, on voit l’image géométrique 0 de la fente, qu’on aurait s’il n’y avait pas de réseau, et de chaque côté de cette image des spectres qui sont des juxtapositions des images de la fente correspondant au maxima d’interférences pour les diverses longueurs d’ondes présentes dans la lumière (fig. 8). Dans les montages par réflexion, on peut remplacer le réseau plan par un réseau concave et supprimer l’optique auxiliaire pour former l’image spectrale.Puisque le réseau donne des spectres, il peut remplacer les prismes, en particulier dans les domaines de l’infrarouge et de l’ultraviolet, pour lesquels il n’existe pas de substance transparente et où l’on peut employer des réseaux par réflexion.Principaux types de réseauxLe réseau R est caractérisé par sa largeur L, son pas p et le profil des sillons. Si on reprend le montage de la figure 8, une source ponctuelle, placée au foyer L1, produit une onde plane, parallèle au plan R du réseau. Avant traversée du réseau, tous les points sont en phase.On envisagera trois types de réseaux.Réseau de fentesLes fentes étant très fines, les rayons ne sont diffractés que dans des plans perpendiculaires à la plus grande dimension de chaque fente. On est alors ramené à un problème à une dimension. Si f 0(x ) caractérise la transparence d’une fente:
La figure de diffraction a pour centre: u = u 0, v=v0. Elle suit l’image géométrique de la source dans ses déplacements.Diffraction inverseÀ partir des caractéristiques de l’objet et des pupilles, on peut déterminer la répartition des amplitudes dans l’image. Le problème de la diffraction inverse consiste à déduire les caractéristiques de l’objet à partir des ondes diffractées et enregistrées par le détecteur.2. Les réseauxDescriptionD’une façon générale, un réseau est une surface, transparente ou réfléchissante, présentant une perturbation périodique. Les réseaux possèdent la propriété de disperser la lumière. (Tout le monde a pu observer les spectres colorés qui entourent les ampoules de lampadaires, la nuit, lorsqu’on regarde ceux-ci à travers la trame régulière d’un voilage de fenêtre.)Les premiers réseaux, inventés par Fraunhofer, étaient constitués par des fils équidistants tendus entre deux supports; Fraunhofer bobinait un fil fin entre deux tiges filetées parallèles, soudait les fils sur les tiges, et coupait une des deux nappes de fils ainsi constituées. On peut considérer de tels réseaux comme une série de fentes parallèles et équidistantes; on les utilisait par transmission.Ensuite les réseaux furent fabriqués en gravant, sur une surface de verre ou de métal réfléchissant, une série de sillons équidistants, au moyen d’un diamant; on obtient ainsi des réseaux par transmission, ou par réflexion, difficilement assimilables à une série de fentes, mais dont on peut dire qu’ils ont une structure périodique.Actuellement on fabrique surtout des réseaux par réflexion, obtenus en gravant une série de sillons équidistants dans une mince couche d’aluminium déposée sur une plaque de verre; cette couche d’aluminium étant relativement tendre, on peut, sans que l’usure modifie le profil du diamant traceur, tracer un grand nombre de sillons de profil exactement déterminé à l’avance. On peut d’ailleurs facilement faire des répliques des réseaux ainsi fabriqués par gravure et dont le prix de revient serait trop élevé. La réplique d’un réseau original s’obtient en versant sur le réseau une solution de collodion dans l’éther. Après évaporation de l’éther, on détache du réseau une pellicule transparente qui en reproduit les traits. Une réplique transparente peut être transformée en réplique utilisable par réflexion en y déposant une mince couche métallique par évaporation sous vide.Récemment une technique toute différente, utilisant la photographie, a été mise au point. On obtient un réseau sinusoïdal en enregistrant sur une émulsion photosensible un interférogramme; il suffit de photographier le champ d’un interféromètre à deux ondes, éclairé par une source très monochromatique (un laser). Toutefois, il faut utiliser des plaques spéciales, dites plaques holographiques , qui possèdent une très haute résolution (1 200 à 1 500 traits par mm).Si l’on éclaire un réseau par un faisceau provenant d’une source ponctuelle infiniment éloignée (ou placée au foyer d’une lentille collimatrice), on trouve qu’il y a de la lumière réfléchie (ou transmise) non seulement dans la direction de réflexion régulière (ou de transmission rectiligne), mais aussi dans un certain nombre d’autres directions très bien déterminées qui sont des maxima d’interférences. Or les positions de ces maxima dépendent de la longueur d’onde: on obtient ainsi une dispersion. On ne considérera que des réseaux présentant une perturbation périodique suivant une dimension; on peut alors remplacer la source ponctuelle par une fente parallèle aux sillons du réseau: cette fente est placée dans le plan focal d’une lentille L1, et l’observation s’effectue dans le plan focal d’une lentille L2 placée après le réseau. Si on éclaire la fente en lumière polychromatique, on voit l’image géométrique 0 de la fente, qu’on aurait s’il n’y avait pas de réseau, et de chaque côté de cette image des spectres qui sont des juxtapositions des images de la fente correspondant au maxima d’interférences pour les diverses longueurs d’ondes présentes dans la lumière (fig. 8). Dans les montages par réflexion, on peut remplacer le réseau plan par un réseau concave et supprimer l’optique auxiliaire pour former l’image spectrale.Puisque le réseau donne des spectres, il peut remplacer les prismes, en particulier dans les domaines de l’infrarouge et de l’ultraviolet, pour lesquels il n’existe pas de substance transparente et où l’on peut employer des réseaux par réflexion.Principaux types de réseauxLe réseau R est caractérisé par sa largeur L, son pas p et le profil des sillons. Si on reprend le montage de la figure 8, une source ponctuelle, placée au foyer L1, produit une onde plane, parallèle au plan R du réseau. Avant traversée du réseau, tous les points sont en phase.On envisagera trois types de réseaux.Réseau de fentesLes fentes étant très fines, les rayons ne sont diffractés que dans des plans perpendiculaires à la plus grande dimension de chaque fente. On est alors ramené à un problème à une dimension. Si f 0(x ) caractérise la transparence d’une fente: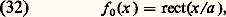 l’amplitude transmise f (x ) par le réseau est obtenue en translatant N fois, de p , la fonction f 0(x ) (N = nombre de traits du réseau = L/p ):
l’amplitude transmise f (x ) par le réseau est obtenue en translatant N fois, de p , la fonction f 0(x ) (N = nombre de traits du réseau = L/p ):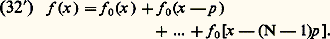
 L’équation (33) peut encore s’écrire:
L’équation (33) peut encore s’écrire: D’où la répartition des éclairements suivant l’axe des u :
D’où la répartition des éclairements suivant l’axe des u :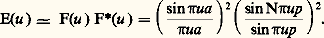 L’intensité diffractée dans la direction i est donc:
L’intensité diffractée dans la direction i est donc: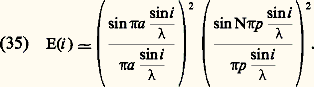 D’une manière générale, l’intensité diffractée peut s’écrire:
D’une manière générale, l’intensité diffractée peut s’écrire: avec:
avec: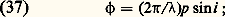 﨏 représente le déphasage entre deux rayons homologues qui sont passés par deux points du réseau distants de p et qui sont diffractés dans la même direction i.L’expression (36) est donnée par le produit de deux termes: le premier représente le phénomène de diffraction dû à un élément du réseau; le deuxième représente les interférences entre les N ondes identiques diffractées par les N éléments du réseau.La figure 9 montre les variations d’éclairement dans l’image de diffraction pour différents cas (cet éclairement est normalisé, c’est-à-dire que la valeur maximale est prise égale à l’unité).On peut remarquer que la diffraction par un élément du réseau module le phénomène d’interférences et que les maxima d’interférences sont obtenus lorsqu’on a des interférences totalement constructives:
﨏 représente le déphasage entre deux rayons homologues qui sont passés par deux points du réseau distants de p et qui sont diffractés dans la même direction i.L’expression (36) est donnée par le produit de deux termes: le premier représente le phénomène de diffraction dû à un élément du réseau; le deuxième représente les interférences entre les N ondes identiques diffractées par les N éléments du réseau.La figure 9 montre les variations d’éclairement dans l’image de diffraction pour différents cas (cet éclairement est normalisé, c’est-à-dire que la valeur maximale est prise égale à l’unité).On peut remarquer que la diffraction par un élément du réseau module le phénomène d’interférences et que les maxima d’interférences sont obtenus lorsqu’on a des interférences totalement constructives: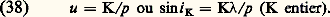 Ces maxima occupent la même position quel que soit le nombre de fentes. Les différentes images d’ordre K sont distantes de:
Ces maxima occupent la même position quel que soit le nombre de fentes. Les différentes images d’ordre K sont distantes de: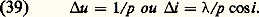 Leur largeur est donnée par:
Leur largeur est donnée par: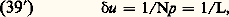 soit: 嗀i =/L cos i . 嗀i ne dépend que de l’angle de diffraction i et de la largeur totale L du réseau; le pas et le profil du réseau n’interviennent pas. Le nombre de maxima d’interférences est limité par le fait que l’on doit avoir [cf. INTERFÉRENCES LUMINEUSES]:
soit: 嗀i =/L cos i . 嗀i ne dépend que de l’angle de diffraction i et de la largeur totale L du réseau; le pas et le profil du réseau n’interviennent pas. Le nombre de maxima d’interférences est limité par le fait que l’on doit avoir [cf. INTERFÉRENCES LUMINEUSES]: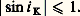 Les ordres d’interférence sont mis en évidence géométriquement sur la figure 10. La remarque, faite ici, est valable pour tous les phénomènes de diffraction. La transformée de Fourier est un outil puissant qui permet d’exprimer très rapidement le principe d’Huygens, mais il ne faut jamais perdre de vue que les coordonnées réduites dépendent de la longueur d’onde et des angles de diffraction. Après avoir effectué les calculs en coordonnées réduites, il est indispensable de passer aux coordonnées réelles, et de tenir compte des conditions expérimentales du montage.La répartition d’énergie n’est pas la même dans tous les ordres. On peut arriver à concentrer l’énergie dans une seule image à condition de donner aux sillons un «profil» approprié.Si l’on remplace S par une fente fine F, on observe dans le plan focal de L2 des raies de largeur 嗀i .Réseau écheletteConsidérons le cas d’un réseau échelette utilisé par réflexion; la section droite de chaque sillon est un triangle rectangle. On suppose que les rayons incidents sont perpendiculaires aux facettes planes telles que AB (fig. 11). La formule (36) est toujours valable. Le terme de diffraction [sin ( 神a sin i )/] / [( 神a sin i )/] reste inchangé, mais la différence de phase entre deux rayons homologues est maintenant:
Les ordres d’interférence sont mis en évidence géométriquement sur la figure 10. La remarque, faite ici, est valable pour tous les phénomènes de diffraction. La transformée de Fourier est un outil puissant qui permet d’exprimer très rapidement le principe d’Huygens, mais il ne faut jamais perdre de vue que les coordonnées réduites dépendent de la longueur d’onde et des angles de diffraction. Après avoir effectué les calculs en coordonnées réduites, il est indispensable de passer aux coordonnées réelles, et de tenir compte des conditions expérimentales du montage.La répartition d’énergie n’est pas la même dans tous les ordres. On peut arriver à concentrer l’énergie dans une seule image à condition de donner aux sillons un «profil» approprié.Si l’on remplace S par une fente fine F, on observe dans le plan focal de L2 des raies de largeur 嗀i .Réseau écheletteConsidérons le cas d’un réseau échelette utilisé par réflexion; la section droite de chaque sillon est un triangle rectangle. On suppose que les rayons incidents sont perpendiculaires aux facettes planes telles que AB (fig. 11). La formule (36) est toujours valable. Le terme de diffraction [sin ( 神a sin i )/] / [( 神a sin i )/] reste inchangé, mais la différence de phase entre deux rayons homologues est maintenant: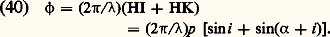 Il en résulte que le maximum de diffraction ne coïncide plus avec l’image d’interférence d’ordre 0. Sur la figure 12 on a représenté la répartition des éclairements dans le cas où a = 4 猪, 見 = 100 et = 2 猪.Les calculs que l’on a présentés ne sont qu’approchés, mais ils montrent la possibilité de concentrer l’énergie dans un ordre d’interférences. De tels réseaux sont dits blazés .Réseau sinusoïdalCe réseau est constitué par une plaque photographique qui a été impressionnée par un système de franges sinusoïdales de pas p . Une fois développée, la plaque possède les propriétés d’un hologramme, c’est-à-dire qu’elle transmet une amplitude f (x ) proportionnelle à l’éclairement qui l’a impressionnée:
Il en résulte que le maximum de diffraction ne coïncide plus avec l’image d’interférence d’ordre 0. Sur la figure 12 on a représenté la répartition des éclairements dans le cas où a = 4 猪, 見 = 100 et = 2 猪.Les calculs que l’on a présentés ne sont qu’approchés, mais ils montrent la possibilité de concentrer l’énergie dans un ordre d’interférences. De tels réseaux sont dits blazés .Réseau sinusoïdalCe réseau est constitué par une plaque photographique qui a été impressionnée par un système de franges sinusoïdales de pas p . Une fois développée, la plaque possède les propriétés d’un hologramme, c’est-à-dire qu’elle transmet une amplitude f (x ) proportionnelle à l’éclairement qui l’a impressionnée: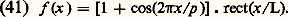 L’amplitude diffractée est donnée par:
L’amplitude diffractée est donnée par: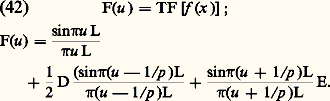 On observe seulement trois images (fig. 13): l’image centrale d’ordre 0 et deux images symétriques d’ordre + 1 et 漣 1 telles que:
On observe seulement trois images (fig. 13): l’image centrale d’ordre 0 et deux images symétriques d’ordre + 1 et 漣 1 telles que: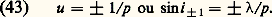 Ces images sont quatre fois moins brillantes que l’image centrale, mais leur largeur reste toujours égale à:
Ces images sont quatre fois moins brillantes que l’image centrale, mais leur largeur reste toujours égale à: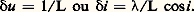 Dispersion et pouvoir de résolution d’un réseauLa formule fondamentale (38) montre que les positions des maxima dépendent de (sauf pour K = 0). Il y a donc dispersion si on éclaire la fente d’entrée avec une source de lumière polychromatique. Le maximum central n’est pas dispersé (puisqu’il contient toutes les radiations de la source), mais les autres maxima donneront des spectres colorés d’ordre + 1, + 2, + 3..., 漣 1, 漣 2, 漣 3... L’aptitude d’un réseau à produire cette dispersion est caractérisée par sa dispersion angulaire:
Dispersion et pouvoir de résolution d’un réseauLa formule fondamentale (38) montre que les positions des maxima dépendent de (sauf pour K = 0). Il y a donc dispersion si on éclaire la fente d’entrée avec une source de lumière polychromatique. Le maximum central n’est pas dispersé (puisqu’il contient toutes les radiations de la source), mais les autres maxima donneront des spectres colorés d’ordre + 1, + 2, + 3..., 漣 1, 漣 2, 漣 3... L’aptitude d’un réseau à produire cette dispersion est caractérisée par sa dispersion angulaire:
 D’une manière générale, si l’onde plane incidente fait l’angle i 0 avec le plan du réseau, on a:
D’une manière générale, si l’onde plane incidente fait l’angle i 0 avec le plan du réseau, on a: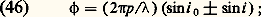 ce qui permet d’écrire:
ce qui permet d’écrire: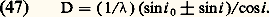 Cette formule montre que la dispersion ne dépend que des angles sous lesquels le réseau est utilisé.Si la source émet deux radiations monochromatiques1 et2 (1 漣2 = d), on aura, dans chaque ordre d’interférence, deux pics distants de di . Si ces deux pics sont très voisins, l’observateur est incapable de les distinguer. On admet qu’ils sont résolus lorsque leur distance angulaire di est supérieure à leur largeur 嗀i , autrement dit, en tenant compte de (39 ), (44) et (45), si di 閭 嗀i , c’est-à-dire:
Cette formule montre que la dispersion ne dépend que des angles sous lesquels le réseau est utilisé.Si la source émet deux radiations monochromatiques1 et2 (1 漣2 = d), on aura, dans chaque ordre d’interférence, deux pics distants de di . Si ces deux pics sont très voisins, l’observateur est incapable de les distinguer. On admet qu’ils sont résolus lorsque leur distance angulaire di est supérieure à leur largeur 嗀i , autrement dit, en tenant compte de (39 ), (44) et (45), si di 閭 嗀i , c’est-à-dire: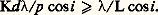 On définit le pouvoir de résolution 倫 du réseau par le rapport/d:
On définit le pouvoir de résolution 倫 du réseau par le rapport/d: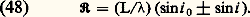 Le pouvoir de résolution d’un réseau ne dépend que de sa largeur et des angles d’utilisation.Application à la spectroscopieLe système dispersif utilisé dans les spectrographes est soit un réseau, soit un prisme. Les réseaux sont utiles dans une gamme de longeurs d’ondes très étendue: depuis l’infrarouge, où ils remplacent les prismes de matières fragiles, telles que les halogénures alcalins, jusqu’à l’ultraviolet lointain où ils permettent le travail dans le vide (lorsque l’on atteint les longueurs d’ondes absorbables par l’air) et même aux rayons X. On rencontre alors deux difficultés: la longueur d’onde est très petite et la dispersion très faible; d’autre part, les rayons X ne se réfléchissent convenablement que sous incidence rasante.Ces deux difficultés sont heureusement résolues si l’on utilise l’incidence rasante. Cette méthode permet de mesurer la longueur d’onde des radiations X.Le pouvoir de résolution du réseau (surtout si l’on travaille dans un ordre élevé) est très nettement supérieur à celui du prisme. Toutefois, le fait que la lumière émise par la source se répartisse en plusieurs spectres confère au réseau moins de luminosité qu’au prisme; ce dernier, en effet, ne donne qu’un seul spectre dans lequel est concentrée toute l’énergie. Autrefois, les astronomes, qui étudiaient des sources de faible luminosité, préféraient utiliser des systèmes à prisme. Actuellement, les réseaux «blazés» offrent la même luminosité que les prismes. Donc, en général, les systèmes à réseaux présentent une incontestable supériorité sur les systèmes à prismes.3. Filtrage des fréquences spatialesÉclairage spatialement cohérentDans tout ce qui suit on supposera que la lumière est monochromatique.Considérons un système afocal constitué par deux lentilles L1 et L2 (supposées identiques pour simplifier). Soit F leur foyer commun. On éclaire le système avec une onde plane (éclairage spatialement cohérent) provenant d’une source ponctuelle à l’infini ou d’un faisceau laser. Si les lentilles L1 et L2 sont très «ouvertes» de façon à ne pas introduire de diffraction, on observe en F un point lumineux et la lentille L2 transmet une onde plane identique à l’onde incidente. Plaçons maintenant un objet dans le plan (O); ce plan coïncide avec le plan focal objet de L1 (fig. 14). Dans le plan focal image de L1 (plan 神), on n’observe plus un point, mais une tache lumineuse appelée spectre ; cela s’explique par la diffraction de l’onde plane incidente par l’objet. Dans le plan (I) conjugué du plan (O), l’image observée doit être identique à l’objet.En réalité, la pupille placée dans le plan ( 神) a des dimensions finies. Elle agit comme un filtre qui supprime certaines fréquences spatiales du spectre. Il en résulte que l’image n’est jamais identique à l’objet. On peut dire que tout instrument d’optique se ramène au schéma suivant:– introduction des données (signaux) dans le plan de l’objet;– filtrage des fréquences spatiales dans le plan de Fourier;– obtention d’une image (réponse), en général différente de l’objet.Nous allons voir sur un exemple simple le mécanisme de la formation des images.Résolution des objets périodiquesOn contrôle habituellement la qualité des instruments en déterminant leur pouvoir de résolution pour un objet de structure périodique, par exemple une mire de Foucault , constituée par des traits blancs équidistants, séparés par des intervalles noirs de même largeur. Si l’éclairage est cohérent (c’est le cas sur un microscope dont le condenseur est très diaphragmé), une telle mire fonctionne comme un réseau et diffracte dans diverses directions. De façon générale, l’amplitude diffractée dans l’objectif est donnée par la transformée de Fourier de la transparence de l’objet. Reprenons la formule (34) dans laquelle on choisit a = p /2. Les maxima d’interférence se produisent dans les directions i K telles que: sin i K = 0,/p , 3/p , 5/p... On dit que 0, 1/p , 3/p , 5/p... sont les fréquences spatiales caractéristiques de l’objet.Toujours à partir de la même relation, on voit que ces fréquences spatiales ont pour amplitude 1, 1/2, 1/6, 1/10... (fig. 15). La pupille ( 神) de l’objectif agit comme un filtre d’amplitude. Elle se comporte comme un filtre passe bas , c’est-à-dire qu’elle ne laisse passer que les basses fréquences spatiales. Abbe, le premier, a montré l’influence de ce filtre sur la structure de l’image (fig. 16 a et 16 b). Désignons par f (x ) la répartition des amplitudes dans l’objet (équation 32) et par f (x ) la répartition des amplitudes dans l’image. Envisageons les cas où le diaphragme laisse passer:– uniquement la fréquence fondamentale; le plan image est uniformément éclairé: il est impossible de détecter la structure périodique de l’objet (fig. 17 a);
Le pouvoir de résolution d’un réseau ne dépend que de sa largeur et des angles d’utilisation.Application à la spectroscopieLe système dispersif utilisé dans les spectrographes est soit un réseau, soit un prisme. Les réseaux sont utiles dans une gamme de longeurs d’ondes très étendue: depuis l’infrarouge, où ils remplacent les prismes de matières fragiles, telles que les halogénures alcalins, jusqu’à l’ultraviolet lointain où ils permettent le travail dans le vide (lorsque l’on atteint les longueurs d’ondes absorbables par l’air) et même aux rayons X. On rencontre alors deux difficultés: la longueur d’onde est très petite et la dispersion très faible; d’autre part, les rayons X ne se réfléchissent convenablement que sous incidence rasante.Ces deux difficultés sont heureusement résolues si l’on utilise l’incidence rasante. Cette méthode permet de mesurer la longueur d’onde des radiations X.Le pouvoir de résolution du réseau (surtout si l’on travaille dans un ordre élevé) est très nettement supérieur à celui du prisme. Toutefois, le fait que la lumière émise par la source se répartisse en plusieurs spectres confère au réseau moins de luminosité qu’au prisme; ce dernier, en effet, ne donne qu’un seul spectre dans lequel est concentrée toute l’énergie. Autrefois, les astronomes, qui étudiaient des sources de faible luminosité, préféraient utiliser des systèmes à prisme. Actuellement, les réseaux «blazés» offrent la même luminosité que les prismes. Donc, en général, les systèmes à réseaux présentent une incontestable supériorité sur les systèmes à prismes.3. Filtrage des fréquences spatialesÉclairage spatialement cohérentDans tout ce qui suit on supposera que la lumière est monochromatique.Considérons un système afocal constitué par deux lentilles L1 et L2 (supposées identiques pour simplifier). Soit F leur foyer commun. On éclaire le système avec une onde plane (éclairage spatialement cohérent) provenant d’une source ponctuelle à l’infini ou d’un faisceau laser. Si les lentilles L1 et L2 sont très «ouvertes» de façon à ne pas introduire de diffraction, on observe en F un point lumineux et la lentille L2 transmet une onde plane identique à l’onde incidente. Plaçons maintenant un objet dans le plan (O); ce plan coïncide avec le plan focal objet de L1 (fig. 14). Dans le plan focal image de L1 (plan 神), on n’observe plus un point, mais une tache lumineuse appelée spectre ; cela s’explique par la diffraction de l’onde plane incidente par l’objet. Dans le plan (I) conjugué du plan (O), l’image observée doit être identique à l’objet.En réalité, la pupille placée dans le plan ( 神) a des dimensions finies. Elle agit comme un filtre qui supprime certaines fréquences spatiales du spectre. Il en résulte que l’image n’est jamais identique à l’objet. On peut dire que tout instrument d’optique se ramène au schéma suivant:– introduction des données (signaux) dans le plan de l’objet;– filtrage des fréquences spatiales dans le plan de Fourier;– obtention d’une image (réponse), en général différente de l’objet.Nous allons voir sur un exemple simple le mécanisme de la formation des images.Résolution des objets périodiquesOn contrôle habituellement la qualité des instruments en déterminant leur pouvoir de résolution pour un objet de structure périodique, par exemple une mire de Foucault , constituée par des traits blancs équidistants, séparés par des intervalles noirs de même largeur. Si l’éclairage est cohérent (c’est le cas sur un microscope dont le condenseur est très diaphragmé), une telle mire fonctionne comme un réseau et diffracte dans diverses directions. De façon générale, l’amplitude diffractée dans l’objectif est donnée par la transformée de Fourier de la transparence de l’objet. Reprenons la formule (34) dans laquelle on choisit a = p /2. Les maxima d’interférence se produisent dans les directions i K telles que: sin i K = 0,/p , 3/p , 5/p... On dit que 0, 1/p , 3/p , 5/p... sont les fréquences spatiales caractéristiques de l’objet.Toujours à partir de la même relation, on voit que ces fréquences spatiales ont pour amplitude 1, 1/2, 1/6, 1/10... (fig. 15). La pupille ( 神) de l’objectif agit comme un filtre d’amplitude. Elle se comporte comme un filtre passe bas , c’est-à-dire qu’elle ne laisse passer que les basses fréquences spatiales. Abbe, le premier, a montré l’influence de ce filtre sur la structure de l’image (fig. 16 a et 16 b). Désignons par f (x ) la répartition des amplitudes dans l’objet (équation 32) et par f (x ) la répartition des amplitudes dans l’image. Envisageons les cas où le diaphragme laisse passer:– uniquement la fréquence fondamentale; le plan image est uniformément éclairé: il est impossible de détecter la structure périodique de l’objet (fig. 17 a);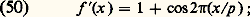 l’image n’est alors pas conforme à l’objet, mais l’on voit apparaître une structure périodique (fig. 17 b);– un grand nombre de fréquences spatiales; on a une image qui ressemble de plus en plus à l’objet.De toute façon, les fréquences élevées, qui fournissent les détails de l’objet, sont toujours supprimées par l’objectif. En éclairage cohérent, l’objectif impose une loi de filtrage représentée sur la figure 18. On voit que la fréquence de coupure est 1/p c, autrement dit la période limite, perceptible dans l’objet, est p c. La transparence en amplitude de la pupille porte le nom de fonction de transfert .Il est possible d’ajouter, dans le plan de la pupille, un filtre adapté de façon à améliorer le contraste de l’image.Filtre adaptéConsidérons un objet faiblement contrasté. L’amplitude de la fréquence fondamentale est beaucoup plus importante que celle des autres fréquences. Les détails de l’image, noyés dans un «fond» lumineux, ne sont pas perceptibles. Par contre, si, dans le plan de la pupille, on place un filtre d’amplitude supprimant ou atténuant la fréquence fondamentale, on peut augmenter le contraste de l’image (cette méthode a été mise au point, en France, par A. Maréchal).On peut utiliser un filtre qui supprime certaines fréquences gênantes dans une image; c’est le cas des photographies tramées qui présentent, dans deux directions perpendiculaires, une périodicité à la fréquence 1/p de la trame. Il suffit de supprimer le «spectre» de la trame avec un écran pour retrouver l’image initiale.Certains objets sont qualifiés d’objets de phase , car, d’un point à un autre, on ne rencontre que des variations de phase (variations d’épaisseur ou variations d’indice, ou les deux à la fois) et pas de variations d’absorption. L’amplitude qu’ils transmettent ou réfléchissent est de la forme:
l’image n’est alors pas conforme à l’objet, mais l’on voit apparaître une structure périodique (fig. 17 b);– un grand nombre de fréquences spatiales; on a une image qui ressemble de plus en plus à l’objet.De toute façon, les fréquences élevées, qui fournissent les détails de l’objet, sont toujours supprimées par l’objectif. En éclairage cohérent, l’objectif impose une loi de filtrage représentée sur la figure 18. On voit que la fréquence de coupure est 1/p c, autrement dit la période limite, perceptible dans l’objet, est p c. La transparence en amplitude de la pupille porte le nom de fonction de transfert .Il est possible d’ajouter, dans le plan de la pupille, un filtre adapté de façon à améliorer le contraste de l’image.Filtre adaptéConsidérons un objet faiblement contrasté. L’amplitude de la fréquence fondamentale est beaucoup plus importante que celle des autres fréquences. Les détails de l’image, noyés dans un «fond» lumineux, ne sont pas perceptibles. Par contre, si, dans le plan de la pupille, on place un filtre d’amplitude supprimant ou atténuant la fréquence fondamentale, on peut augmenter le contraste de l’image (cette méthode a été mise au point, en France, par A. Maréchal).On peut utiliser un filtre qui supprime certaines fréquences gênantes dans une image; c’est le cas des photographies tramées qui présentent, dans deux directions perpendiculaires, une périodicité à la fréquence 1/p de la trame. Il suffit de supprimer le «spectre» de la trame avec un écran pour retrouver l’image initiale.Certains objets sont qualifiés d’objets de phase , car, d’un point à un autre, on ne rencontre que des variations de phase (variations d’épaisseur ou variations d’indice, ou les deux à la fois) et pas de variations d’absorption. L’amplitude qu’ils transmettent ou réfléchissent est de la forme: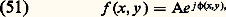 comme les récepteurs usuels (rétine, émulsion photosensible, cellule photo-électrique...) ne sont sensibles qu’aux variations d’éclairement, l’image d’un tel objet présente un éclairement constant donné par:
comme les récepteurs usuels (rétine, émulsion photosensible, cellule photo-électrique...) ne sont sensibles qu’aux variations d’éclairement, l’image d’un tel objet présente un éclairement constant donné par: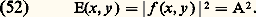 Il est cependant très important de percevoir des objets de phase: pour les métallurgistes qui observent des états de surface, pour les biologistes qui observent des cellules vivantes que les méthodes classiques de coloration peuvent détruire.Si un objet de phase reçoit une onde plane, l’onde transmise (ou réfléchie) n’est pas plane, mais présente des accidents locaux dus aux différences de phase introduites par l’objet. Les méthodes que nous allons décrire s’appliquent au cas où les dimensions de ces accidents sont petites et où les déphasages sont faibles.Considérons le montage de la figure 19. Les rayons qui sont passés en dehors du défaut H viennent converger au point F, alors que le détail déphasant M diffracte la lumière que la lentille L2 concentre au point M . En M interfèrent la lumière directe, qui produit un fond cohérent, et la lumière diffractée.Revenons à l’équation (51), (on supposera A = 1 pour simplifier). Étant donné que 﨏(x , y ) est petit, on peut écrire que l’amplitude transmise par l’objet est de la forme:
Il est cependant très important de percevoir des objets de phase: pour les métallurgistes qui observent des états de surface, pour les biologistes qui observent des cellules vivantes que les méthodes classiques de coloration peuvent détruire.Si un objet de phase reçoit une onde plane, l’onde transmise (ou réfléchie) n’est pas plane, mais présente des accidents locaux dus aux différences de phase introduites par l’objet. Les méthodes que nous allons décrire s’appliquent au cas où les dimensions de ces accidents sont petites et où les déphasages sont faibles.Considérons le montage de la figure 19. Les rayons qui sont passés en dehors du défaut H viennent converger au point F, alors que le détail déphasant M diffracte la lumière que la lentille L2 concentre au point M . En M interfèrent la lumière directe, qui produit un fond cohérent, et la lumière diffractée.Revenons à l’équation (51), (on supposera A = 1 pour simplifier). Étant donné que 﨏(x , y ) est petit, on peut écrire que l’amplitude transmise par l’objet est de la forme: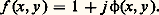 L’amplitude diffractée dans le plan de Fourier est de la forme:
L’amplitude diffractée dans le plan de Fourier est de la forme: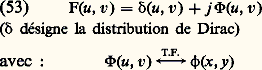 Si la lentille L2 ne diaphragme pas, l’amplitude dans le plan image est identique à celle de l’objet, d’où l’éclairement dans ce plan:
Si la lentille L2 ne diaphragme pas, l’amplitude dans le plan image est identique à celle de l’objet, d’où l’éclairement dans ce plan: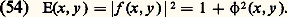 Puisque 﨏 est petit, l’éclairement au point M est très peu différent de l’éclairement en un point voisin de M . Le contraste de l’image, défini par:
Puisque 﨏 est petit, l’éclairement au point M est très peu différent de l’éclairement en un point voisin de M . Le contraste de l’image, défini par: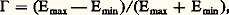 est de l’ordre de 﨏2, ce qui montre bien qu’un tel objet de phase n’est pas perceptible (fig. 20 a).Plaçons au point F une petite pastille opaque qui arrête toute la lumière directe (observation par strioscopie ), on a:
est de l’ordre de 﨏2, ce qui montre bien qu’un tel objet de phase n’est pas perceptible (fig. 20 a).Plaçons au point F une petite pastille opaque qui arrête toute la lumière directe (observation par strioscopie ), on a: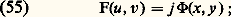 d’où:
d’où: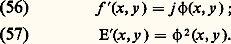 L’intensité en M est donc égale à 﨏2, elle est nulle partout ailleurs. On voit pourquoi la strioscopie porte aussi le nom de méthode du fond noir (fig. 20 b). Le contraste est maximal et toujours égal à 1. Malheureusement, 﨏 et, par conséquent, 﨏2 sont très petits. Par cette méthode, on peut détecter la présence d’un déphasage, mais il est difficile de le mesurer. D’autre part, il est impossible de connaître le signe de 﨏 (avance ou retard de phase). La méthode du contraste de phase est beaucoup plus avantageuse. Remplaçons en F la pastille opaque par une lame de phase , parfaitement transparente, qui déphase les rayons directs de + 神/2. Juste après cette lame de phase, la répartition d’amplitude est de la forme:
L’intensité en M est donc égale à 﨏2, elle est nulle partout ailleurs. On voit pourquoi la strioscopie porte aussi le nom de méthode du fond noir (fig. 20 b). Le contraste est maximal et toujours égal à 1. Malheureusement, 﨏 et, par conséquent, 﨏2 sont très petits. Par cette méthode, on peut détecter la présence d’un déphasage, mais il est difficile de le mesurer. D’autre part, il est impossible de connaître le signe de 﨏 (avance ou retard de phase). La méthode du contraste de phase est beaucoup plus avantageuse. Remplaçons en F la pastille opaque par une lame de phase , parfaitement transparente, qui déphase les rayons directs de + 神/2. Juste après cette lame de phase, la répartition d’amplitude est de la forme: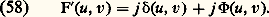 D’où la répartition des amplitudes dans le plan image:
D’où la répartition des amplitudes dans le plan image: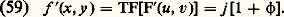 L’éclairement dans le plan (I) est donné par:
L’éclairement dans le plan (I) est donné par: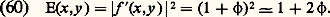 Le contraste est proportionnel à 2 﨏. La méthode donne correctement le signe de 﨏. On peut améliorer considérablement la sensibilité en mettant en F une lame de phase absorbante. Le module de l’amplitude transmise est alors t . Dans le plan de Fourier, on a alors la répartition d’amplitude:
Le contraste est proportionnel à 2 﨏. La méthode donne correctement le signe de 﨏. On peut améliorer considérablement la sensibilité en mettant en F une lame de phase absorbante. Le module de l’amplitude transmise est alors t . Dans le plan de Fourier, on a alors la répartition d’amplitude: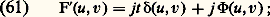 d’où:
d’où: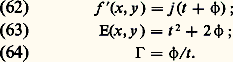 臨 peut augmenter beaucoup si t est choisi suffisamment grand. Le contraste de phase permet de mettre en évidence des différences de marche de l’ordre du dixième de nanomètre (fig. 20 c).Il est facile de réaliser, par holographie, des filtres qui agissent à la fois sur la phase et sur l’amplitude des fréquences spatiales. Ils sont utilisés pour la reconnaissance des formes et la reconnaissance des caractères.Éclairage spatialement incohérentDans le cas de l’éclairage spatialement cohérent, on pouvait considérer que deux points arbitrairement choisis dans l’objet émettaient des vibrations présentant entre elles une différence de phase constante (définie par la différence des chemins optiques qui les séparent de la source). Pour connaître la répartition des amplitudes dans l’image, il suffisait d’appliquer le principe de Huygens et d’ajouter les amplitudes vibratoires provenant de chaque point de l’objet. Dans le cas de l’éclairage spatialement incohérent [cf. INTERFÉRENCES LUMINEUSES], chaque point de l’objet émet des vibrations incohérentes. La répartition des éclairements dans l’image s’obtient en faisant la somme des éclairements produits par les images des divers points de l’objet.Utilisons un système de grandissement 1, tel celui qui est schématisé sur la figure 14. Désignons par M(x , y ) un point courant du plan objet (O) et par M (x , y ) un point courant du plan image (I). Si O(M) représente la répartition de l’intensité dans le plan objet et D(M) la répartition des éclairements dans la tache de diffraction, l’intensité au point M de l’image sera donnée par:
臨 peut augmenter beaucoup si t est choisi suffisamment grand. Le contraste de phase permet de mettre en évidence des différences de marche de l’ordre du dixième de nanomètre (fig. 20 c).Il est facile de réaliser, par holographie, des filtres qui agissent à la fois sur la phase et sur l’amplitude des fréquences spatiales. Ils sont utilisés pour la reconnaissance des formes et la reconnaissance des caractères.Éclairage spatialement incohérentDans le cas de l’éclairage spatialement cohérent, on pouvait considérer que deux points arbitrairement choisis dans l’objet émettaient des vibrations présentant entre elles une différence de phase constante (définie par la différence des chemins optiques qui les séparent de la source). Pour connaître la répartition des amplitudes dans l’image, il suffisait d’appliquer le principe de Huygens et d’ajouter les amplitudes vibratoires provenant de chaque point de l’objet. Dans le cas de l’éclairage spatialement incohérent [cf. INTERFÉRENCES LUMINEUSES], chaque point de l’objet émet des vibrations incohérentes. La répartition des éclairements dans l’image s’obtient en faisant la somme des éclairements produits par les images des divers points de l’objet.Utilisons un système de grandissement 1, tel celui qui est schématisé sur la figure 14. Désignons par M(x , y ) un point courant du plan objet (O) et par M (x , y ) un point courant du plan image (I). Si O(M) représente la répartition de l’intensité dans le plan objet et D(M) la répartition des éclairements dans la tache de diffraction, l’intensité au point M de l’image sera donnée par: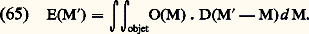 Cette opération est une convolution que l’on écrit:
Cette opération est une convolution que l’on écrit: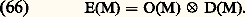 (Pour plus de détails, on se reportera au traité de diffraction de Maréchal et Françon, mentionné en bibliographie). D’après le théorème de Parseval, la transformée de Fourier de E(M) est le produit des transformées de Fourier de O(M) et D(M), soit:
(Pour plus de détails, on se reportera au traité de diffraction de Maréchal et Françon, mentionné en bibliographie). D’après le théorème de Parseval, la transformée de Fourier de E(M) est le produit des transformées de Fourier de O(M) et D(M), soit: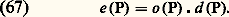 La transformée de Fourier de l’image est égale au produit de la transformée de l’objet par la transformée de l’image du point isolé.D’après (67), on voit que les fréquences spatiales o (P) qui caractérisent l’objet sont affectées par le coefficient d (P). On peut dire que la loi de filtrage de l’instrument est régie par d (P), qui porte le nom de fonction de transfert de l’instrument (en éclairage incohérent).Si A(M) caractérise la répartition des amplitudes dans la tache de diffraction, on a:
La transformée de Fourier de l’image est égale au produit de la transformée de l’objet par la transformée de l’image du point isolé.D’après (67), on voit que les fréquences spatiales o (P) qui caractérisent l’objet sont affectées par le coefficient d (P). On peut dire que la loi de filtrage de l’instrument est régie par d (P), qui porte le nom de fonction de transfert de l’instrument (en éclairage incohérent).Si A(M) caractérise la répartition des amplitudes dans la tache de diffraction, on a: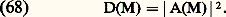 On sait que A(H) est la transformée de Fourier de l’amplitude f (P) transmise par le pupille. On peut donc écrire:
On sait que A(H) est la transformée de Fourier de l’amplitude f (P) transmise par le pupille. On peut donc écrire: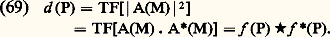 La fonction de transfert est donnée par la fonction d’autocorrélation de la transparence (en amplitude) de la pupille.Sur la figure 18 on a représenté la fonction de transfert d’un instrument diaphragmé par une pupille en forme de fente. On voit que la fréquence limite est double de celle qui est admise dans le cas de l’éclairage cohérent. Il en résulte qu’un instrument éclairé avec une source spatialement incohérente a une résolution meilleure qu’un instrument éclairé avec une source cohérente. (En microscopie, on ouvre au maximum le condenseur pour faire apparaître les plus fins détails de la préparation.) Toutefois, la courbe de réponse montre une décroissance de l’amplitude de modulation.
La fonction de transfert est donnée par la fonction d’autocorrélation de la transparence (en amplitude) de la pupille.Sur la figure 18 on a représenté la fonction de transfert d’un instrument diaphragmé par une pupille en forme de fente. On voit que la fréquence limite est double de celle qui est admise dans le cas de l’éclairage cohérent. Il en résulte qu’un instrument éclairé avec une source spatialement incohérente a une résolution meilleure qu’un instrument éclairé avec une source cohérente. (En microscopie, on ouvre au maximum le condenseur pour faire apparaître les plus fins détails de la préparation.) Toutefois, la courbe de réponse montre une décroissance de l’amplitude de modulation.
Encyclopédie Universelle. 2012.
